De paradox van de maatregelen

Leestijd: 6 minuten

Nu de corona epidemie op zijn eind loopt, wordt het tijd om eens wat conclusies te trekken, met name wat betreft het effect van de maatregelen die de overheid heeft genomen. De basis van deze maatregelen werd gevormd door de modellen van het RIVM, die voorspelden dat deze succesvol bleven, zolang ze gehandhaafd zouden blijven.

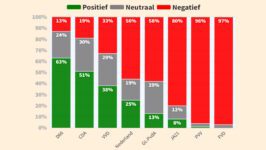
In het Catshuis werden door prof. Van Dissel vele voorbeelden gepresenteerd wat er zou gebeuren als de maatregelen niet werden gevolgd, bijvoorbeeld deze op 25 oktober 2020:

En deze op 6 maart 2021:

R0 is gebonden aan moment afhankelijke factoren

Als Green Team hebben we op basis van ziekenhuisopnamecijfers laten zien wat de invloed is van het seizoen in ons blog Wat is de seizoeninvloed en hieruit bleek dat de R0 geen constante waarde heeft zoals vaak gedacht wordt, maar afhankelijk is van meerdere factoren:

• De virologische eigenschappen van het virus
• Seizoeninvloed: gedurende de wintermaanden verspreidt het virus zich makkelijker
• Weerbaarheid: in de zomer vindt er opbouw plaats van weerbaarheid, het immuunsysteem wordt sterker, vitamine D etc.
• Opkomst van nieuwe varianten, de Engelse variant is daarvan de bekendste
• Menselijke factoren/gedragingen
• Maatregelen

Merk op dat vaccinatie in dit lijstje niet is opgenomen. Wij beschouwen dit als onderdeel van de opbouw van immuniteit, die dan weer de waarde van de effectieve R-waarde (R_eff) bepaalt. Afgezien van de virologische eigenschappen van het virus, zijn alle factoren een functie van de tijd.

In deze grafiek zien we de opbouw van de immuniteit vergeleken met het niveau van de benodigde immuniteit.
De blauwe lijn is de totale immuniteit en wordt berekend uit het totaal aantal ziekenhuisopnames ten opzichte van de gehele bevolking.
Omdat de R0 niet constant is in de tijd maar afhankelijk is van verschillende invloeden, is de opgebouwde immuniteit soms voldoende om besmettingen te doen dalen, maar op andere momenten juist niet. We kunnen nu vanuit de R0 berekenen wat per moment de immuniteit zou moeten zijn om het aantal besmettingen constant te houden, dit noemen we de ‘benodigde immuniteit’ en dat is de blauwe stippellijn.
Als de opgebouwde immuniteit onder het benodigde immuniteitsniveau zit, dan stijgen de besmettingen. Dat is van juli tot november het geval (met uitzondering van 2 weken hittegolf in augustus) en dus stijgen de cijfers. Vanaf november zien we dat er een soort evenwicht ontstaat tussen de beide blauwe lijnen, waardoor een golvend patroon ontstaat. Het benodigde immuniteitsniveau stijgt voortdurend, onder invloed van alle hierboven genoemde factoren.

Deze grafiek is een benadering van de werkelijkheid die waarschijnlijk gecompliceerder is, maar voor het begrip volstaat deze grafiek!

Lockdowns werken zichzelf tegen

De vraag die we willen beantwoorden is welke rol de maatregelen nu spelen bij de verspreiding van het virus. Eigenlijk valt deze vraag uiteen in twee delen:

1. Welke invloed hebben de maatregelen op het moment dat ze afgekondigd worden. We gebruiken de kennis en cijfers van het RIVM als uitgangspunt.
2. Maar de andere veel belangrijkere vraag is: wat is het uiteindelijke effect op de verdere verspreiding van covid-19 op de langere termijn? Hiervoor gebruiken wij de rekenregels van de epidemiologen.

Wat we hebben gedaan, is het veronderstelde percentage verlaging van de R-waarde in rekening gebracht bij de R0-waarde. Ter controle hebben we eerst het verloop van de epidemie gereconstrueerd, enkel en alleen uitgaande van de R0-waarde en de wetmatigheid voor de verspreiding van een virus. Deze gereconstrueerde curve komt inderdaad vrijwel overeen met de waargenomen aantallen ziekenhuisopnames.

De volgende stap is dan het verlagen van de R0-waarde gedurende de periode dat een maatregel werkzaam is. Als voorbeeld hebben we de effectiviteit van de avondklok gekozen. Daarvan is door het RIVM gezegd dat deze een effect van 10% zou hebben op het reproductiegetal. Deze maatregel is normaal gesproken onderdeel van een pakket aan maatregelen, dus hebben wij ervoor gekozen om hier 5% voor te nemen. Deze keuze is niet essentieel, het gaat meer om het principe dan om de juistheid van de cijfers zoals we later zullen zien.

De avondklok is ingegaan op 23 januari 2021 en geëindigd op 28 april 2021. Alle R0 waarden tussen deze data zijn in onze berekeningen met 5% verlaagd en vervolgens is de curve voor het aantal ziekenhuisopnames opnieuw bepaald. Dit lijkt nu een paradox, want de R0-curve was al berekend op basis van een maatregel die al was ingevoerd en dit zou dus een dubbel effect zijn. Om hieraan tegemoet te komen, is ook een lijn berekend, die het tegenovergestelde effect laat zien, dus geen reductie, maar juist een stijging van de R0 van 5%. Dit is dan het plaatje dat we gaan krijgen:

Groen is de 5% verlaagde R0 en rood de 5% verhoogde. De gele lijn is de gereconstrueerde curve voor het aantal ziekenhuisopnames zoals NICE die dagelijks rapporteert.

De Paradox

We kunnen nu twee situaties gaan evalueren met behulp van deze drie lijnen:

1. Stel dat de maatregel precies het beoogde effect heeft. De gele curve is dan kennelijk het resultaat. Als de maatregel niet zou zijn doorgevoerd (rood), dan was de R0 van 23 januari tot 28 april 5% hoger geweest en dan hadden we dus op 23 januari een plotselinge stijging gezien en dat komt overeen met de rode stippellijn. We zien daarna vanaf maart juist een snellere daling als gevolg van de extra opgebouwde immuniteit. Dit model wordt in de politiek ook wel de Preventieparadox genoemd.
2. Stel dat de maatregel geen enkel effect heeft. Ook dan volgen we de gele lijn, want dat zijn de waarnemingen geweest. Als er wel een gunstig effect geweest zou zijn (groen), dan hadden we de groene stippellijn gevolgd die 5% lager ligt. Echter, we zien dan wel dat er dan in maart een nieuwe piek zou ontstaan, omdat er minder opbouw van immuniteit zou zijn geweest.

Als we nu de totaalaantallen ziekenhuisopnames van de twee verschillende scenario’s gaan vergelijken, dan zien we zelfs dat het totaalaantal ziekenhuisopnames met avondklok 2% hoger is dan zonder het effect van de avondklok (rood vergeleken met geel, of geel vergeleken met groen) en dat lijkt dus paradoxaal.

Uiteraard kunnen we ook andere percentages en duur van de maatregel gaan vergelijken, maar de uitkomst zal altijd dezelfde zijn: een maatregel bepaalt de duur van de epidemie en (vrijwel) niet het aantal ziekenhuisopnames. Lockdowns werken zichzelf tegen.

Effectiviteit mondkapjes

Op geheel vergelijkbare wijze kunnen we het effect van het dragen van mondkapjes uitbeelden. Het effect wordt weliswaar door het RIVM ingeschat als gering, maar het zou er wel zijn. We nemen even aan dat het 1% is. De mondkapjes zijn verplicht per 1 december en deze datum nemen we dan ook als begindatum van deze maatregel. Dit wordt dan de grafiek voor de mondkapjes:

We zien hier hetzelfde beeld als bij de avondklok: eerst enige tijd het beoogde beeld (groene stippellijn), maar daarna treedt er een inhaaleffect op. Het nettoresultaat is dat het aantal ziekenhuisopnames daalt met 0,03%, een bijna verwaarloosbare opbrengst.

Ab Osterhaus

Als curiosa ook nog het voorstel van Ab Osterhaus om een aantal weken een stevige lockdown te houden. Op 13 oktober werden er door de regering strengere maatregelen aangekondigd, waarop Osterhaus met het voorstel voor stevigere lockdown.

We hebben zijn voorstel vertaald in een stevige lockdown van een maand, ingaande 13 oktober 2020 en met een enorme reductie van de R0 van 50% (streng is dan inderdaad streng, iedereen alleen naar buiten met een geldige reden etc.). Dit zou dan het resultaat geweest zijn:

We zien hier inderdaad de halvering van de R0 gedurende 31 dagen en daardoor een enorme daling van het aantal ziekenhuisopnames met op 13 november nog maar 1 opname per dag zijn en het aantal besmette mensen op die dag is dan nog slechts 750. Maar in de maanden erna groeit het aantal besmettingen weer gewoon door en door de achterstand in de ontwikkeling van immuniteit krijgen we in februari een piek die net zo hard aangroeit als die in maart en zal niet alleen leiden tot uiteindelijk 8% meer ziekenhuisopnames maar ook een vervijfvoudiging van het aantal ziekenhuisopnames in maart. Ook hier een Lockdown die zichzelf tegenwerkt.

Vaccinatie

We hebben het hier nog niet gehad over de rol van vaccinatie. Dat is een ingewikkeld verhaal. Omdat, zoals we eerder hebben gezien, de R0 en R_eff voortdurend met elkaar in evenwicht proberen te blijven, komt de veronderstelde daling van de R_eff door vaccinatie niet goed uit de verf. Als daar belangstelling voor is, kunnen we daar in een apart blog op terugkomen. Het doet verder aan het principe van de berekening van de effectiviteit van maatregelen niets af.

Conclusies

Het effect van maatregelen op de verspreiding van het covid-19 virus is uiterst beperkt. Kennelijk viert het korte termijn denken hoogtij. We hebben middels een aantal voorbeelden laten zien dat maatregelen niet leiden tot lagere belasting van de ziekenhuizen, maar wel tot grotere spreiding over de tijd.

Maatregelen zijn meer politieke ideologie dan wetenschap.

De enige uitzondering waarbij maatregelen wel nuttig kunnen zijn, is in de sterk opgaande fase van de besmettingen, om te voorkomen dat een zeker maximum aan ziekenhuis capaciteit wordt overschreden. De prijs die ervoor betaald wordt, is het langer duren van de epidemie.